|
До сих пор мы всегда считали, что в незамагниченной плазме может существовать только один высокочастотный резонанс, характеризующий продольные ленгмюровские колебания. Но, поскольку такой резонанс является продольным, то он не может излучать электромагнитные волны.
Однако при взрыве ядерных бомб наблюдается излучение электромагнитных колебаний в очень широком спектре частот. Поэтому возникает вопрос о поиске новых механизмов излучения таких колебаний высокотемпературной плазмой. В работах [1-3] показано, что вещественные уравнения Максвелла для бездиссипативной плазмы имеют вид:
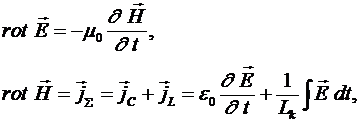 (1) (1)
Второе уравнение соотношений (1) представляет суммарную плотность тока, текущего через плазму, в случае наложения на неё электрических полей. Эта плотность тока состоит из двух составляющих: емкостной и индуктивной, наподобие тому, как это имеет место в параллельном колебательном контуре. В указанных работах показано, что эквивалентная схема плазмы представляет из себя параллельный колебательный резонансный контур. Такой подход особенно понятен специалистам радиотехнических специальностей.
Но применение уравнений Максвелла для решения задач электродинамики приобретает смысл, если известны граничные условия. Поэтому решим конкретную задачу для двух параллельных полуплоскостей, ширину которых обозначим буквой 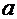 , а расстояние между ними – буквой , а расстояние между ними – буквой  . .
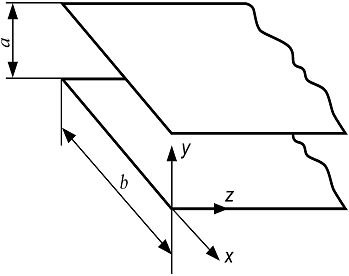
Если линия расположена в вакууме, то погонная (приходящаяся на единицу длины) индуктивность и ёмкость такой линии без учёта краевых эффектов определяются соотношениями
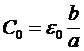 (2) (2)
и
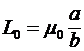 , (3) , (3)
поэтому с ростом длины линии ее суммарная емкость
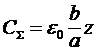 (4) (4)
и суммарная индуктивность
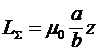 (5) (5)
увеличиваются пропорционально ее длине  . .
Если в разомкнутую линию поместить плазму, носители заряда в которой могут двигаться без трения, и в поперечном направлении пропустить через плазму ток 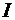 , то заряды, двигаясь с определенной скоростью, будут запасать кинетическую энергию. Поскольку плотность тока определяется соотношением , то заряды, двигаясь с определенной скоростью, будут запасать кинетическую энергию. Поскольку плотность тока определяется соотношением
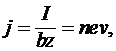 (6) (6)
то суммарная кинетическая энергия всех движущихся зарядов запишется
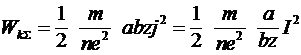 . (7) . (7)
Соотношение (7) связывает энергию, запасенную в линии, с квадратом тока, поэтому коэффициент, стоящий в правой части соотношения (7) перед квадратом тока, является суммарной индуктивностью линии.
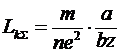 .(8) .(8)
Таким образом, величина
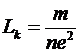 (9) (9)
представляет удельную кинетическую индуктивность. Соотношение (9) получено для случая постоянного тока, когда токовое распределение является однородным.
Из соотношения (8) видно, что в отличие от  величина величина  с ростом с ростом 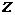 уменьшается. С физической точки зрения это понятно, связано это с тем, что с ростом уменьшается. С физической точки зрения это понятно, связано это с тем, что с ростом 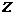  количество параллельно включенных индуктивных элементов растет. количество параллельно включенных индуктивных элементов растет.
Эквивалентная схема линии, заполненной бездиссипативной плазмой, будет эквивалентна параллельному колебательному контуру с сосредоточенными параметрами:
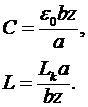 (10) (10)
Но если вычислить резонансную частоту такого контура, то окажется, что эта частота вообще ни от каких размеров не зависит, действительно:
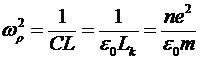 . (11) . (11)
Мы получили очень интересный результат, который говорит о том, что резонансная частота рассмотренного макроскопического резонатора не зависит от его размеров. Может создаться впечатление, что мы имеем дело с ленгмюровским резонансом, т.к. полученное значение резонансной частоты в точности соответствует значению частоты ленгмюровского резонанса. Но мы знаем, что такой резонанс характеризует продольные волны, в то время как в длинной линии мы имеем дело с распространением поперечной волны. Для данного случая величина фазовой скорости в направлении 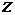 равна бесконечности и волновой вектор равна бесконечности и волновой вектор 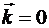 . Данный результат соответствует решению системы уравнений (8) для линии с заданной конфигурацией. Из соотношений (9) следует, что волновое число определяется соотношением . Данный результат соответствует решению системы уравнений (8) для линии с заданной конфигурацией. Из соотношений (9) следует, что волновое число определяется соотношением
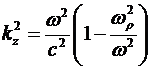 , (12) , (12)
а групповая и фазовая скорости соотношениями
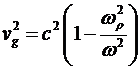 , (13) , (13)
 , (14) , (14)
где 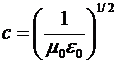 – скорость света в вакууме. – скорость света в вакууме.
Для такой плазмы фазовая скорость электромагнитной волны равна бесконечности. Следовательно, в каждый момент времени распределение полей и токов в такой линии однородно и не зависит от координаты  , а ток в плоскостях линии в этом направлении отсутствует. Это означает, что в данном случае вместо проводящих плоскостей могут быть использованы любые плоскости, ограничивающие плазму сверху и снизу. Отметим, что пока мы обсуждаем только принципиальную сторону вопроса, т.к., например, газоразрядную плазму ограничить для данных целей плоскостями нельзя, т.к. на эти плоскости будут оседать заряды. Возможно, это должна быть плазма в твердом теле, или газоразрядная плазма в магнитной ловушке, , а ток в плоскостях линии в этом направлении отсутствует. Это означает, что в данном случае вместо проводящих плоскостей могут быть использованы любые плоскости, ограничивающие плазму сверху и снизу. Отметим, что пока мы обсуждаем только принципиальную сторону вопроса, т.к., например, газоразрядную плазму ограничить для данных целей плоскостями нельзя, т.к. на эти плоскости будут оседать заряды. Возможно, это должна быть плазма в твердом теле, или газоразрядная плазма в магнитной ловушке,
Из соотношений (12) , (13) и (14) нетрудно видеть, что в точке 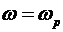 мы имеем дело с поперечным резонансом с бесконечной добротностью. То, что в отличие от ленгмюровского, данный резонанс является поперечным, будет хорошо видно для случая, когда добротность такого резонанса не будет равна бесконечности. В этом случае мы имеем дело с поперечным резонансом с бесконечной добротностью. То, что в отличие от ленгмюровского, данный резонанс является поперечным, будет хорошо видно для случая, когда добротность такого резонанса не будет равна бесконечности. В этом случае 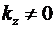 , и в линии будет распространяться поперечная волна, направление распространения которой будет перпендикулярно направлению движения зарядов. Конечно, рассмотрение данной задачи мы начали с рассмотрения плазмы, ограниченной с двух сторон плоскостями длинной линии. Но в процессе такого рассмотрения мы пришли к выводу, что наличие такого резонанса вообще от размеров линии не зависит. Значит, резонанс должен наблюдаться и в безграничной среде. Таким образом, в безграничной плазме кроме ленгмюровского резонанса, характеризующего продольные волны, может существовать и поперечный резонанс. Поскольку частоты этих резонансов совпадают, то они являются вырожденными. Отметим, что факт существования такого резонанса ранее осознан не был и это явление нигде описано не было. , и в линии будет распространяться поперечная волна, направление распространения которой будет перпендикулярно направлению движения зарядов. Конечно, рассмотрение данной задачи мы начали с рассмотрения плазмы, ограниченной с двух сторон плоскостями длинной линии. Но в процессе такого рассмотрения мы пришли к выводу, что наличие такого резонанса вообще от размеров линии не зависит. Значит, резонанс должен наблюдаться и в безграничной среде. Таким образом, в безграничной плазме кроме ленгмюровского резонанса, характеризующего продольные волны, может существовать и поперечный резонанс. Поскольку частоты этих резонансов совпадают, то они являются вырожденными. Отметим, что факт существования такого резонанса ранее осознан не был и это явление нигде описано не было.
Перед тем, как перейти к более подробному рассмотрению данного вопроса, остановимся на энергетических процессах, имеющих место в плазме в случае отсутствия потерь.
Характеристическое сопротивление плазмы, дающее отношение поперечных компонент электрического и магнитного полей, определяется соотношением
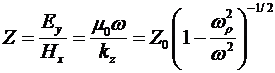 , (15) , (15)
где 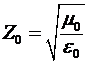 – характеристическое сопротивление вакуума. – характеристическое сопротивление вакуума.
Полученное значение 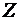 характерно для поперечных электрических волн в волноводах. Видно, что когда характерно для поперечных электрических волн в волноводах. Видно, что когда 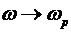 , то , то 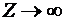 , a , a 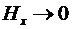 . В том случае, когда . В том случае, когда 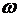 > >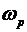 в плазме существует и электрическая и магнитная составляющая поля. Удельная энергия этих полей запишется в плазме существует и электрическая и магнитная составляющая поля. Удельная энергия этих полей запишется
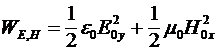 (16) (16)
Таким образом, энергия, заключенная в магнитном поле, в 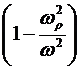 раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что такое рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волны электрического и магнитного полей, несущей электрическую и магнитную энергию в плазме распространяется еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что такое рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волны электрического и магнитного полей, несущей электрическую и магнитную энергию в плазме распространяется еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается
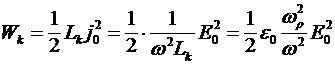 . (17) . (17)
Таким образом, полная удельная энергия записывается так:
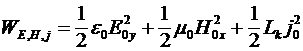 . (18) . (18)
Следовательно, для нахождения полной удельной энергии, запасенной в единице объема плазмы, учет только полей 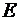 и и 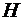 недостаточен. недостаточен.
В точке 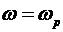 выполняется соотношение выполняется соотношение
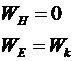 (19) (19)
т.е. магнитное поле в плазме отсутствует, и плазма представляет из себя макроскопический электромеханический резонатор с бесконечной добротностью, резонирующий на частоте 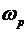 . .
Поскольку при частотах 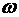 > >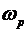 волна, распространяющаяся в плазме, несет на себе три вида энергии: магнитную, электрическую и кинетическую, то такую волну можно назвать магнитноэлектрокинетической. Кинетическая волна представляет из себя волну плотности тока волна, распространяющаяся в плазме, несет на себе три вида энергии: магнитную, электрическую и кинетическую, то такую волну можно назвать магнитноэлектрокинетической. Кинетическая волна представляет из себя волну плотности тока
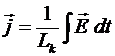 . (20) . (20)
Эта волна сдвинута по отношению к электрической на p/2.
До сих пор мы рассматривали физически нереализуемый случай, когда потери в плазме отсутствуют, что соответствует бесконечной добротности плазменного резонатора. Если потери имеются, причем совершенно неважно какими физическими процессами такие потери обусловлены, то добротность плазменного резонатора будет конечной величиной. Для такого случая уравнения Максвелла будут иметь вид:
 (21) (21)
Наличие потерь учитывается членом 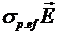 , причем, употребляя возле проводимости индекса , причем, употребляя возле проводимости индекса 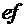 , мы тем самым подчеркиваем, что нас не интересует сам механизм потерь, а интересует только сам факт их существования. Величину , мы тем самым подчеркиваем, что нас не интересует сам механизм потерь, а интересует только сам факт их существования. Величину  определяет добротность плазменного резонатора. Для измерения определяет добротность плазменного резонатора. Для измерения 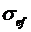 мы должны выбрать отрезок линии длиной мы должны выбрать отрезок линии длиной  , величина которого значительно меньше длины волны в диссипативной плазме. Такой отрезок будет эквивалентен контуру с сосредоточенными параметрами: , величина которого значительно меньше длины волны в диссипативной плазме. Такой отрезок будет эквивалентен контуру с сосредоточенными параметрами:
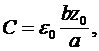 (22) (22)
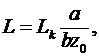 (23) (23)
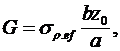 (24) (24)
где 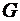 – проводимость, подключенная параллельно – проводимость, подключенная параллельно 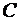 и и 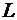 . .
Проводимость и добротность в таком контуре связаны соотношением
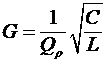 ,(25) ,(25)
откуда, учитывая (22-24), получаем
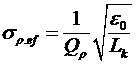 . (26) . (26)
Таким образом, измеряя собственную добротность плазменного резонатора, мы можем определить 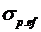 . Используя (26) и (21) получим . Используя (26) и (21) получим
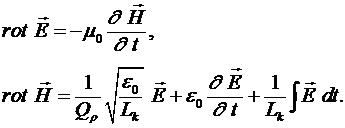 (27) (27)
Рассмотрим решение системы уравнений (27) в точке 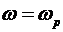 . При этом, поскольку . При этом, поскольку
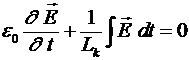 , (28) , (28)
Получаем
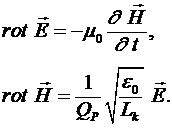 (29) (29)
Решение этой системы уравнений хорошо известно. Амплитуда волны, уходящая вглубь рассматриваемой среды, убывает по закону 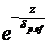 . .
Поскольку при помощи плазмы может быть создан макроскопический одночастотный резонатор, то такой резонатор представляет интерес для разработки и создания электрокинетических лазеров. При достаточно больших значениях 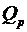 энергия магнитных полей вблизи поперечного резонанса значительно меньше, чем кинетическая энергия носителей тока и энергии электрических полей. Поэтому в первом приближении магнитные поля можем не учитывать. Кроме того, при малых потерях, поперечная фазовая скорость всегда будет значительно больше скорости света. Поэтому, мы можем положить энергия магнитных полей вблизи поперечного резонанса значительно меньше, чем кинетическая энергия носителей тока и энергии электрических полей. Поэтому в первом приближении магнитные поля можем не учитывать. Кроме того, при малых потерях, поперечная фазовая скорость всегда будет значительно больше скорости света. Поэтому, мы можем положить
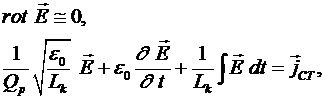 (30) (30)
где 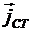 – плотность сторонних токов. – плотность сторонних токов.
Проинтегрировав (23) по времени и разделив обе части на 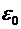 ,, получим ,, получим
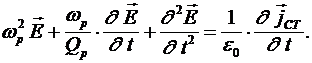 (31) (31)
Если (31) проинтегрировать по поверхности нормальной к вектору 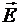 и ввести электрический поток как и ввести электрический поток как  получим получим
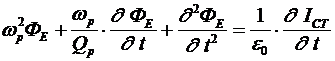 ,(32) ,(32)
где 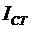 – сторонний ток. – сторонний ток.
Уравнение (32) является уравнением гармонического осциллятора с правой частью, характерное для двухуровневых лазеров. Если источник возбуждения отключить, то мы будем иметь дело с “холодным” лазерным резонатором, в котором колебания будут затухать по экспоненциальному закону
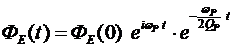 ,(33) ,(33)
т.е. макроскопический электрический поток  будет осциллировать с частотой будет осциллировать с частотой 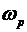 , время релаксации при этом определяется соотношением , время релаксации при этом определяется соотношением
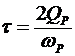 . (34) . (34)
Задача создания лазера на таком резонаторе заключается теперь лишь в умении возбудить такой резонатор.
Если резонатор возбуждается сторонними токами, то такой резонатор для этих токов представляет полосовой фильтр с резонансной частотой равной плазменной частоте с полосой пропускания
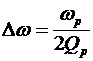 . (35) . (35)
Меняя плотность носителей зарядов в плазме, можно перестраивать резонансную частоту такого фильтра. Эта особенность может служить основой для создания полосовых фильтров с быстрой перестройкой частоты. Схема такого фильтра очень проста. Газоразрядную плазму ионизируют посредством СВЧ сигнала, меняя мощность которого, меняют частоту резонансного фильтра.
На этой основе могут быть также построены индикаторы и измерители жесткого гамма излучения. Если газоразрядную плазму дополнительно облучать гамма излучением, то плотность свободных носителей зарядов в ней будет меняться, что повлечет за собой изменение частоты плазменного резонанса.
Другим важным практическим применением поперечного плазменного резонанса является возможность его использование для разогрева и диагностики плазмы. Если добротность плазменного резонатора велика, что может быть достигнуто при высокой проводимости плазмы, то в таком резонаторе могут быть получены высокие уровни электрических полей, а значит и высокие энергии носителей зарядов.
Таким образом, поперечный плазменный резонанс может быть использован для решения ряда различных практических задач, о существовании таких возможностей до публикации перечисленных ниже работ известно не было.
1. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков,
Константа, 2003.- 72 с. ISBN 966-7983-55-2.
2. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, –
153 с. ISBN 978-966-8603-23-5. http://fmnauka.narod.ru/link3.html
3. Transversal plasma resonance in a nonmagnetized plasma and possibilities of
practical employment of it. http://arxiv.org/abs/physics/0506081
|
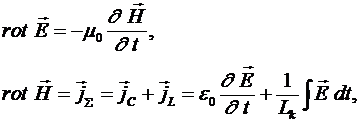 (1)
(1)
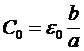 (2)
(2)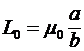 , (3)
, (3)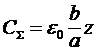 (4)
(4)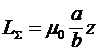 (5)
(5)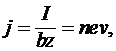 (6)
(6)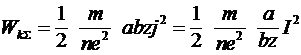 . (7)
. (7) 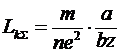 .(8)
.(8) 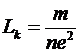 (9)
(9) 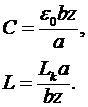 (10)
(10)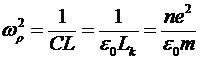 . (11)
. (11)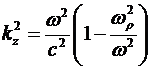 , (12)
, (12) 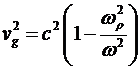 , (13)
, (13)  , (14)
, (14) 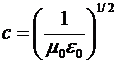 – скорость света в вакууме.
– скорость света в вакууме.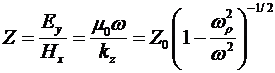 , (15)
, (15)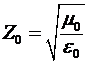 – характеристическое сопротивление вакуума.
– характеристическое сопротивление вакуума.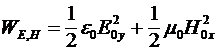 (16)
(16)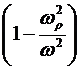 раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что такое рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волны электрического и магнитного полей, несущей электрическую и магнитную энергию в плазме распространяется еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается
раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что такое рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волны электрического и магнитного полей, несущей электрическую и магнитную энергию в плазме распространяется еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается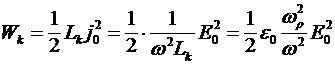 . (17)
. (17)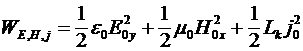 . (18)
. (18)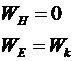 (19)
(19)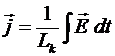 . (20)
. (20)  (21)
(21) 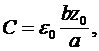 (22)
(22) 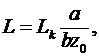 (23)
(23) 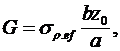 (24)
(24) 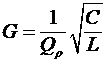 ,(25)
,(25)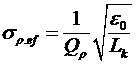 . (26)
. (26) 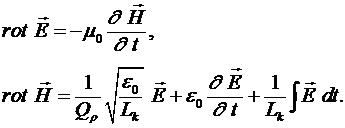 (27)
(27) 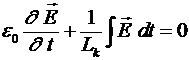 , (28)
, (28)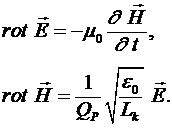 (29)
(29) 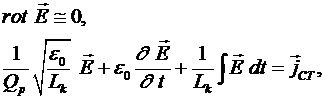 (30)
(30) 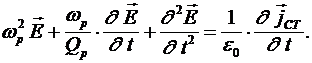 (31)
(31) 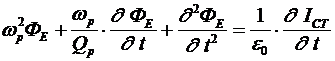 ,(32)
,(32) 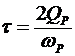 . (34)
. (34)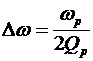 . (35)
. (35)