|
Известно, что процессы распространения электромагнитных волн в свободном пространстве описывают уравнения Максвелла, из которых следуют волновые уравнения. В длинных линиях для этих целей пользуются телеграфными уравнениями. И те и другие представляют из себя дифференциальные уравнения второго порядка в частных производных. Основной задачей волновых и телеграфных уравнений является нахождение скорости распространения волновых процессов, а также волнового сопротивления среды или длинной линии.
Сейчас мы рассмотрим новый метод получения волновых уравнений для длинных линий, основанный на несколько других принципах.
Рассмотрим процессы, происходящие в длинной линии, в которой емкость и индуктивность являются распределенными параметрами. Положим что удельная (приходящаяся на единицу длины) емкость и удельная индуктивность линии составляют 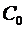 и и 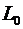 . Теперь предположим, что при подключении к линии источника постоянного напряжения фронт электрического поля в ней движется со скоростью v. Тогда длина линии, заполненной электрическими полями будет меняется в соответствии с законом . Теперь предположим, что при подключении к линии источника постоянного напряжения фронт электрического поля в ней движется со скоростью v. Тогда длина линии, заполненной электрическими полями будет меняется в соответствии с законом 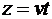 . При этом суммарная величина и емкости линии, и ее индуктивности будут также изменяться по закону . При этом суммарная величина и емкости линии, и ее индуктивности будут также изменяться по закону
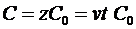 , ,
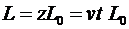 , ,
Если к такой линии подключен источник напряжения 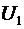 , то он будет заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии должен течь ток , то он будет заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии должен течь ток
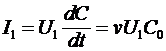 (1) (1)
Этот ток будет течь через проводники линии, обладающие индуктивностью. Но в связи с тем, что сама индуктивность этих проводников тоже увеличивается, то на ней будет иметь место падение напряжения
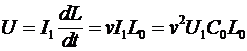 . .
Но падение напряжения на проводниках линии равно напряжению, приложенному к линии, поэтому в последнем выражении следует положить 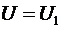 . С учетом этого сразу находим, что скорость распространения фронта электрического поля в линии при заданных погонных параметрах и при наличии на ее входе постоянного напряжения . С учетом этого сразу находим, что скорость распространения фронта электрического поля в линии при заданных погонных параметрах и при наличии на ее входе постоянного напряжения 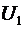 должна составлять должна составлять
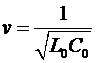 . (2) . (2)
Эта скорость равна скорости распространения фронта волны постоянного напряжения и тока. Процесс в линии происходит таким образом, что фронт волны, распространяясь со скоростью 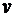 , оставляет за собой линию, заряженную до разности потенциалов , оставляет за собой линию, заряженную до разности потенциалов 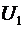 , а на участке линии от источника напряжения до фронта волны течет ток , а на участке линии от источника напряжения до фронта волны течет ток 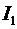 . Величину тока в линии можно получить, подставив значения скорости распространения фронта волны, определяемого соотношением (2), в соотношение (1). Сделав эту подстановку, получим . Величину тока в линии можно получить, подставив значения скорости распространения фронта волны, определяемого соотношением (2), в соотношение (1). Сделав эту подстановку, получим
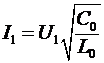 , ,
где
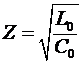
есть волновое сопротивление линии.
Таким образом, процессы распространения постоянного напряжения и постоянного тока в линии являются связанными и взаимно дополняющими процессами, которые существовать друг без друга не могут. Рассмотреную волну мы можем называть электротоковой.
Зная ток и напряжение, мы можем вычислить энергию, приходящуюся на единицу длины линии. Эти энергии будут определяться соотношениями:
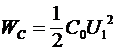 , (3) , (3)
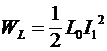 . (4) . (4)
Нетрудно видеть, что 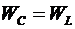 . .
Теперь мы должны обсудить вопрос о длительности фронта электротоковой волны и о том, какое пространство этот фронт будет занимать в самой линии. Ответ на первый вопрос определяется свойствами самого источника напряжения, т.к. локальная производная 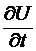 зависит только от переходных процессов в самом источнике. Если процесс установления потенциала на входе линии будет длиться какое-то время зависит только от переходных процессов в самом источнике. Если процесс установления потенциала на входе линии будет длиться какое-то время 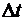 , то в линии он займет участок длиной , то в линии он займет участок длиной 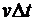 . Если к линии приложить напряжение, меняющееся со временем по закону . Если к линии приложить напряжение, меняющееся со временем по закону 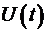 , то это же значение функции будет наблюдаться в любой точке линии на расстоянии , то это же значение функции будет наблюдаться в любой точке линии на расстоянии 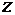 от ее начала с запаздыванием от ее начала с запаздыванием 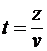 . Таким образом, функция . Таким образом, функция
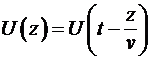 (5) (5)
может быть названа функцией распространения, т.к. она устанавливает связь между временными (локальными) и пространственными значениями функции. На основании функции распространения (5) мы можем установить связь между локальными и пространственными производными в длинной линии. Очевидно, что
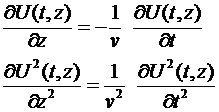 . .
Мы записали соотношения только для производных первого и второго порядка, но подобным же образом могут быть найдены и производные более высоких порядков.
Таким образом, мы получили все те результаты, которые могут быть получены путем решения телеграфных уравнений, и может показаться, что данные решения являются эквивалентными. Это не так. Во-первых, мы получили данные результаты на других принципах, Важно отметить, что сам процесс распространения в данном случае обязан саморасширению электрического поля и тока, в результате чего линия наполняется энергией. Во-вторых, решение волнового уравнения длинных линий
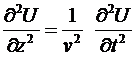 , (6) , (6)
полученное из телеграфных уравнений
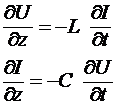 , ,
указывает на то, каким образом распространяются по длинной линии производные тока и напряжения, но никак не указывают на то, каким образом распространяются сами функции. Решение уравнения (6) производится обычно просто путем подбора подходящей функции, без должного понимания физической природы происходящих процессов. Преимущество проведенного рассмотрения заключается в том, что мы имеем ясную физическую картину происходящего.
При рассмотрении процессов в длинной линии у нас фигурировали такие понятия как погонная емкость и индуктивность, а также токи и напряжения в линии. Однако, в электродинамике, основанной на уравнениях Максвелла, нет таких понятий как емкость и индуктивность, а есть понятия электрической и магнитной проницаемости среды. В проведенном рассмотрении также отсутствовали такие понятия как электрические и магнитные поля. Мы сейчас попытаемся для одного конкретного примера связать все указанные параметры. Для этого возьмем простейшую конструкцию линии, расположенную в вакууме, состоящую из двух плоскостей с заданной шириной 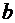 и расстоянием и расстоянием 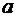 между ними. между ними.
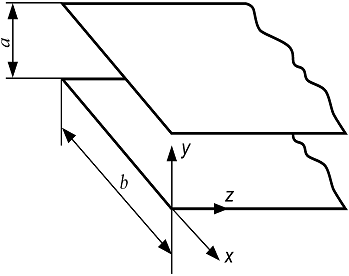
Будем считать, что 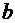 >> >>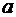 и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями среды, в которой линия расположена, будет существовать следующая связь: и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями среды, в которой линия расположена, будет существовать следующая связь:
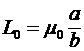 , (7) , (7)
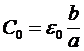 , (8) , (8)
где 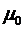 и и 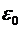 - магнитная и диэлектрическая проницаемость вакуума. Фазовая скорость в такой линии будет определяться соотношением - магнитная и диэлектрическая проницаемость вакуума. Фазовая скорость в такой линии будет определяться соотношением
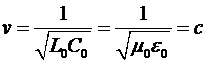 , ,
где 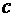 - скорость распространения света в вакууме. Волновое сопротивление рассмотренной линии будет равно - скорость распространения света в вакууме. Волновое сопротивление рассмотренной линии будет равно
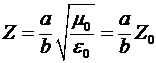 , ,
где
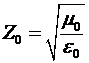
- волновое сопротивление свободного пространства.
Если 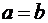 , то без учёта краевых эффектов, электромагнитная волна, распространяющаяся в такой линии, будет по своим характеристикам эквивалентна плоской волне, распространяющейся в свободном пространстве. Особенностью будет то, что в данной линии, в отличие от свободного пространства, может протекать и постоянный ток. А этот случай не может быть рассмотрен путем решения уравнений Максвелла. , то без учёта краевых эффектов, электромагнитная волна, распространяющаяся в такой линии, будет по своим характеристикам эквивалентна плоской волне, распространяющейся в свободном пространстве. Особенностью будет то, что в данной линии, в отличие от свободного пространства, может протекать и постоянный ток. А этот случай не может быть рассмотрен путем решения уравнений Максвелла.
Если к рассмотренной линии бесконечной длины, или линии нагруженной волновым сопротивлением, подключить источник постоянного напряжения 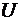 , то напряженность поля в линии составит , то напряженность поля в линии составит
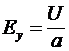 , ,
а ток, текущий в линии будет определяться соотношением
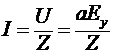 . (9) . (9)
Магнитное поле в линии будет равно удельному току, протекающему в линии
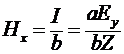 . .
Подставляя сюда значение 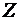 , получаем , получаем
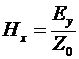 . (10) . (10)
Такая же связь между электрическим и магнитным полем имеет место и для случая электромагнитной волны, распространяющейся в свободном пространстве.
Если мы в (10) подставим (9), и обе части равенства возведем в квадрат, а затем разделим на два, то получим
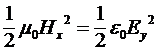 . (11) . (11)
Это означает, что удельная энергия, запасенная в магнитном и электрическом поле в такой линии одинакова. Если значения этих энергий умножить на объемы, занимаемые полями, то полученные величины совпадают с выражениями (3–4).
Таким образом, длинная линия является устройством, которое при подключении к ней источника постоянного  напряжения заполняется двумя видами энергии: электрической и магнитной. Удельные плотности этих энергий равны, а поскольку и электрическая и магнитная энергии заполняют одинаковые объемы, то и общая энергия, запасенная в этих полях одинакова. Особенностью данной линии является то, что при протекании в линии постоянного тока распределение электрического и магнитного полей в ней является однородным. Нетрудно показать, что сила, действующая на проводники такой линии равна нулю. Это следует из соотношения (11), в котором его правая и левая части представляют удельные силы, приложенные к плоскостям линии. Но электрическая и магнитная силы имеют разные знаки, поэтому они компенсируют друг друга. Если к линии приложить напряжение, меняющееся со временем по любому закону напряжения заполняется двумя видами энергии: электрической и магнитной. Удельные плотности этих энергий равны, а поскольку и электрическая и магнитная энергии заполняют одинаковые объемы, то и общая энергия, запасенная в этих полях одинакова. Особенностью данной линии является то, что при протекании в линии постоянного тока распределение электрического и магнитного полей в ней является однородным. Нетрудно показать, что сила, действующая на проводники такой линии равна нулю. Это следует из соотношения (11), в котором его правая и левая части представляют удельные силы, приложенные к плоскостям линии. Но электрическая и магнитная силы имеют разные знаки, поэтому они компенсируют друг друга. Если к линии приложить напряжение, меняющееся со временем по любому закону 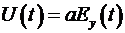 , то по аналогии с (5) можно записать , то по аналогии с (5) можно записать
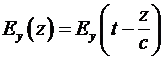 . .
Аналогичное соотношение будет иметь место и для магнитных полей.
Очевидно, что произведение 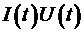 представляет мощность представляет мощность 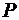 , передаваемую через поперечное сечение линии в направлении , передаваемую через поперечное сечение линии в направлении 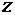 . Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим . Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим 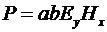 . Величина . Величина 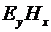 - это абсолютная величина вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии. Конечно, все то, что мы сейчас сделали, можно записать и в векторной форме. - это абсолютная величина вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии. Конечно, все то, что мы сейчас сделали, можно записать и в векторной форме.
Таким образом, все выводы, полученные нами на основании рассмотрения процессов в длинной линии двумя методами, совпадают. Поэтому мы и в дальнейшем, не рискуя допустить ошибки принципиального характера, можем для описания процессов в длинных линиях с успехом пользоваться такими параметрами, как распределенная индуктивность и емкость. Конечно, при этом следует понимать, что 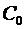 и и 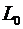 это некоторые интегральные характеристики, не учитывающие структуру полей, и их вычисление может быть осуществлено только на основе знания такой структуры. Следует отметить, что применение параметров это некоторые интегральные характеристики, не учитывающие структуру полей, и их вычисление может быть осуществлено только на основе знания такой структуры. Следует отметить, что применение параметров 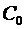 и и 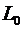 имеет важное практическое значение, т.к. при их помощи могут быть приближенно решены задачи, которые полевым методом решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали. Данная методика получения волновых уравнений рассмотрена в работе [1]. имеет важное практическое значение, т.к. при их помощи могут быть приближенно решены задачи, которые полевым методом решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали. Данная методика получения волновых уравнений рассмотрена в работе [1].
Литература.
1. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, –
153 с. ISBN 978-966-8603-23-5
|
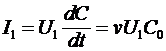 (1)
(1) 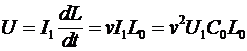 .
.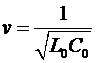 . (2)
. (2) 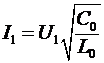 ,
,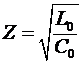
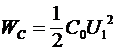 , (3)
, (3) 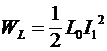 . (4)
. (4) 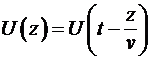 (5)
(5) 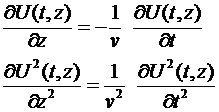 .
.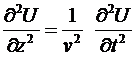 , (6)
, (6) 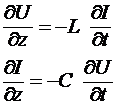 ,
,
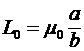 , (7)
, (7) 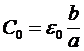 , (8)
, (8) 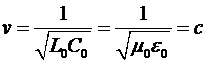 ,
,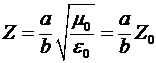 ,
,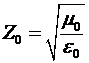
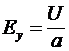 ,
,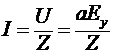 . (9)
. (9) 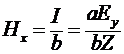 .
.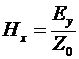 . (10)
. (10) 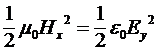 . (11)
. (11) 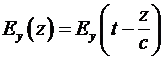 .
.